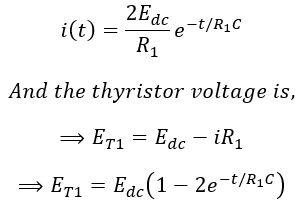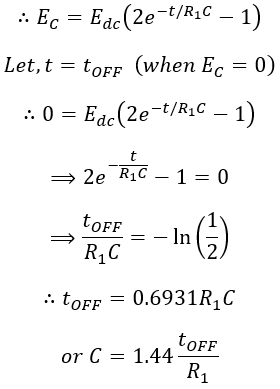In class A and class B commutation methods discussed in the earlier articles, there is only one SCR used, coming to the class-c commutation method there will be two SCRs. One SCR acts as the main thyristor and the other as the auxiliary. It is a type of forced commutation technique that uses additional external components in the circuit for the commutation of the thyristor.

The class-C commutation of the thyristor is also known as complementary impulse commutation or complementary commutation. The name complementary commutation comes after its operation that, the auxiliary thyristor is triggered in order to turn-OFF the main thyristor, while the auxiliary thyristor is turned-OFF when the main thyristor is triggered.

In this method of commutation, a reverse voltage is applied across the thyristor by discharging a capacitor such that it creates reverse bias and helps in commutating the thyristor. Let us see the circuit design and working of class-C or complementary commutation of thyristor or SCR.

Circuit of Class C Commutation :

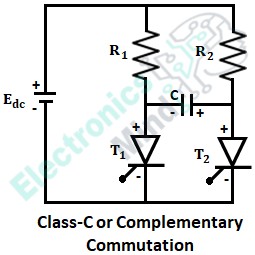
The circuit for class c or complementary commutation is shown in the below figure. The circuit consists of the main thyristor T₁ along with the commutating components that compress capacitor C and complementary thyristor T₂. The load resistance R₁ is connected in series with the main thyristor T₁.

Working of Class C or Complementary Commutation :

Mode-1 :

Initially, the main thyristor T₁, as well as the complementary thyristor T₂, are in the OFF state and the voltage across the capacitor, E_C is zero. In mode-1, the condition of T₁, T₂, and capacitor can be represented as,

Mode-2 :

At ωt = t₀, main thyristor T₁ is triggered due to which the load current starts flowing and also the capacitor C starts charging with the polarities as shown in the figure above. The load current flows through the path,

And the charging capacitor current flows through the path,

In this mode the capacitor is fully charged to the supply voltage i.e., it continues to charge until it gains a voltage equal to the input voltage E_dc. Thus the condition of T₁, T₂, and capacitor in mode-2 will be changed and is represented as,

Mode-3 :

At ωt = t₁, thyristor T₂ is triggered and it starts conducting. The main thyristor T₁ turns OFF immediately after triggering the complementary thyristor T₂ since it will be reverse biased.

When the thyristor T₂ is triggered, the negative polarity of the capacitor C is applied across the anode of T₁ and the positive polarity of capacitor C is applied across the cathode of T₁. This causes to reverse bias the T₁ and thus, thyristor T₂ will conduct and T₁ will be turned OFF i.e., commutation of T₁ is done by turning ON T₂.

Now, the capacitor charges to a voltage equal to -E_dc (from t₁ to t₂) through the load which will be in reverse polarity. The charging path of capacitor C is,

E_dc → R₁ → C → T₂ → E_dc

At the end of mode-3, the state of T₁, T₂ and capacitor becomes,

T₁ is in OFF state, T₂ is in ON state, and E_C = -E_dc

Mode-4 :

At ωt = t₃, thyristor T₁ is again triggered and it starts conducting. Immediately, thyristor T₂ gets commutated since it gets reverse bias voltage due to discharge of capacitor in the reverse direction. Again the capacitor starts to charge as in the case mode-2 and the process continues. By the end of this mode, the condition of T₁, T₂, and capacitor is represented as,

Waveform of Class-C or Complementary Commutation :

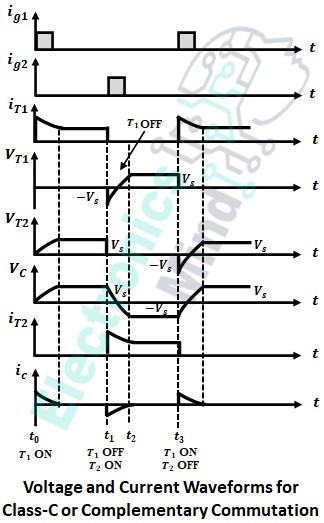
This type of commutation is very useful for frequencies less than 1000 Hz. The waveforms for complementary impulse commutation are shown in the below figure.

In the above waveforms, i_g1 and i_g2 are the gate triggering pulses given to thyristors T₁ and T₂. V_T1 and i_T1 are the voltage and current across thyristor T₁, similarly, V_T2 and i_T2 are the voltage and current across thyristor T₂, and V_C and i_C are the voltage and current of capacitor C.

We can see that, at instant t₁ when triggering pulse i_g1 is given, the thyristor T₁ turns-ON. Hence the voltage drop, V_T1 across T₁ will be zero and there will be the flow of load current i_T1 through T₁. Since the triggering pulse is not given to T₂, the current i_T2 will be zero and the voltage across T₂ will be maximum. Also at the same time, the capacitor charges to the voltage V_C from t₀ to t₁.

Now in order to turn-OFF T₁, thyristor T₂ is triggered at t₂ by applying pulse i_g2. When T₂ turns ON, current i_T2 flows and voltage V_T2 becomes zero. Due to this, capacitor voltage makes the thyristor T₁ reverse bais (from t₁ to t₂) and thus T₁ gets turned OFF. At this condition the supply voltage appears across T₁ as V_T1, current i_T1 becomes zero and the capacitor will charge in reverse direction i.e., to -V_s from t₁ to t₃.

Circuit Design of Class-C Commutation :

To find the current through and the voltage across commutating capacitor, applying KVL to the closed-loop of the capacitor at instant ωt = t₁, i.e., for loop E_dc → R₁ → C → T₂ → E_dc.

Now, applying Inverse Laplace transform for the above equation, we get,

The voltage across the capacitor must be equal to the voltage across the main thyristor T₁ for turning OFF the main thyristor T₁.

The maximum permissible dV/dt across thyristor T₁ using commutation components is given by (dV/dt)_max > 2V/R_LC. Since the commutation of SCR in this method is due to the application of reverse voltage, the class-C commutation is also known as Voltage Commutation. The single-phase inverter circuit that employs centre-tapped transformer uses the class-C method of commutation of SCR.